比特币的数学曲线:揭秘加密货币背后的数学原理

随着数字货币的兴起,比特币作为首个成功的加密货币,其背后的数学原理逐渐成为人们关注的焦点。本文将深入探讨比特币所使用的数学曲线,揭示其安全性和可靠性的数学基础。
一、椭圆曲线密码学简介

椭圆曲线密码学(ECC)是一种基于椭圆曲线数学的密码学分支。与传统的基于大整数的密码学不同,椭圆曲线密码学利用椭圆曲线上的点进行加密和解密。由于其密钥长度较短,但安全性极高,因此在数字货币领域得到了广泛应用。
二、比特币所使用的椭圆曲线

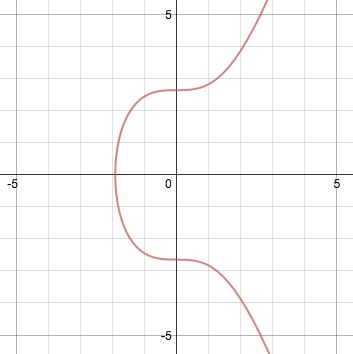
比特币所使用的椭圆曲线被称为secp256k1。这是一种特殊的椭圆曲线,其定义如下:
方程:y^2 = x^3 + ax + b (mod p)
其中,a、b、p是椭圆曲线的参数,x和y是椭圆曲线上的点。在secp256k1中,a=0,b=7,p=0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141。
三、椭圆曲线上的运算

在椭圆曲线上,可以进行加法和乘法运算。加法运算类似于传统的点加法,而乘法运算则利用了椭圆曲线的群性质。在比特币中,这些运算被用于生成公钥和私钥。
1. 加法运算:给定两个点P和Q,它们的和为R。R的坐标可以通过以下公式计算:
R = (x3, y3) = (x1x2y3 - x2x3y1, y1x2y3 - x1x3y2)

2. 乘法运算:给定一个点P和一个整数k,P的k倍为Q。Q的坐标可以通过以下公式计算:
Q = (x3, y3) = (x1^2y3 - ax1^2 - b, y1^2x3 - ax1y1^2 - y2)
四、比特币的私钥和公钥

在比特币中,私钥是一个256位的随机数,用于生成公钥。公钥是私钥在椭圆曲线上的对应点。私钥和公钥之间通过椭圆曲线上的乘法运算相互转换。
1. 生成公钥:给定私钥k和椭圆曲线上的基点G,公钥P可以通过以下公式计算:
P = kG = (x1, y1)
2. 生成私钥:给定公钥P和椭圆曲线上的基点G,私钥k可以通过以下公式计算:
k = (x1x2y3 - x2x3y1) / (x1x2y3 - x2x3y2)

五、比特币的签名算法

比特币的签名算法基于椭圆曲线数字签名算法(ECDSA)。该算法利用椭圆曲线上的运算和哈希函数,确保交易的安全性。
1. 生成消息哈希:将交易信息与魔术字节连接,然后使用SHA-256哈希函数生成消息哈希。
2. 生成签名:使用私钥和椭圆曲线上的运算,对消息哈希进行签名。
3. 验证签名:使用公钥和椭圆曲线上的运算,验证签名是否有效。
比特币的数学曲线是其安全性的基石。通过椭圆曲线密码学,比特币实现了高效且安全的交易。随着数字货币的不断发展,了解比特币的数学原理对于保障其安全性和可靠性具有重要意义。
